SKOS2OWL is an online tool that converts hierarchical classifications available in the W3C SKOS (Simple Knowledge Organization Systems) format into RDF-S or OWL ontologies. In many cases, the resulting ontologies can be used directly. If not, they can be refined using standard ontology engineering tools like e.g. Protégé.
What can SKOS2OWL do for you?
Hierarchical classifications are available for many domains of interest. They often provide a large amount of categories and some sort of hierarchies. Thanks to their size and popularity, they are promising input for putting data on the Semantic Web. Unfortunately, they can mostly not directly be used as ontologies for the Semantic Web and other applications, because classifications are not (or at least: very bad) ontologies. In particular, the labels in categories often lack a context-neutral notion of what it means to be an instance of that category, and the meaning of the hierarchical relations is often not a strict subClassOf.
SKOS2OWL uses the GenTax algorithm described in [1] for deriving, at your choice, either an RDF-S or an OWL ontology from most hierarchical classifications available in the SKOS exchange format. In detail, SKOS2OWL carries out the following steps:
- It helps the user narrow down the intended meaning of the ontology classes.
- It guides the user through several modeling choices. In particular, SKOS2OWL can draw a representative random sample of relevant conceptual elements in the SKOS file and asks the user to make statements about their meaning. This can be used to make reliable modeling decisions without looking at every single element, which would be unfeasible for large classifications.
- It creates an RDF/XML file of the resulting RDF-S or OWL ontology, which can be downloaded.
SKOS2OWL can also be used for creating WSML ontologies from SKOS with the help of the OWL2WSML converter available at http://tools.sti-innsbruck.at/wsml/owl2wsml-translator/.
^ TOPSKOS Simple Knowledge Organization Systems
SKOS stands for "Simple Knowledge Organization Systems" and is a W3C activity to support the use of Knowledge Organization Systems (KOS) for the Semantic Web. For further information and all specifications, please see the official W3C Web page at http://www.w3.org/2004/02/skos/.
^ TOPThe GenTax Algorithm
The GenTax algorithm is an approach for deriving consistent RDF-S and OWL ontologies from hierarchical classifications. It allows for the script-based creation of meaningful ontology classes for a particular context while preserving the original hierarchy, even if the latter is not a real subsumption hierarchy in this particular context. Human intervention in the transformation is limited to checking some conceptual properties and identifying frequent anomalies, and the only input required is an informal categorization plus a notion of the target context. GenTax was developed by Martin Hepp and Jos de Bruijn and first described in [1].
One key property of the approach is that it suggests using representative random samples of the overall classification for choosing appropriate modeling alternatives. This minimizes the amount of human intervention while guaranteeing that the amount of inconsistent elements is below a threshold to be chosen by the user.
In the following, we briefly describe the approach:
- a directed graph
- where nodes represent categories and
- edges represent the "broader term" or "has super-category" relation.
- Depending on the context, a set is related to each category.
- This set represents the items associated with the category in a particular context.
This holds for many hierarchical Knowledge Organization Systems, e.g. the directory structures on our computers or standardized products and services classifications like the UNSPSC.
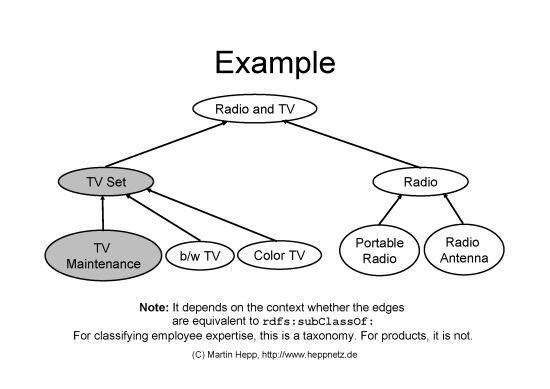
Figure 1 shows such a hierarchical categorization schema.
Figure 1: Example of a hierarchical categorization schema
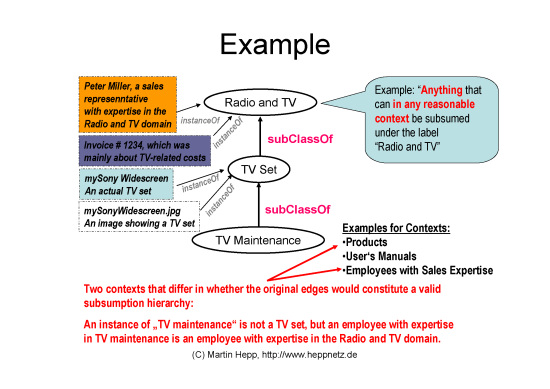
An important observation is that the same hierarchy can be used in different contexts with varying semantics of the categories and / or varying semantics of the hierarchy relations. Figures 2 and 3 explain this in more detail: The category itself has a very broad meaning, approximately that of "Anything that can in any reasonable context be subsumed under the given label". In application contexts, however, people often assume a much narrower meaning for each category - e.g. either products of a certain type, employees that have expertise in a certain area, or invoices that refer to a certain type of goods.
As long as the context of usage is known to both the one who assigns data to those categories and the one who interpretes this data, this does not cause problems. On the Semantic Web, however, we need ontology classes (concepts) that have a context-independent meaning - when we search for TV sets, we may want to find actual TV sets only and not images of TV sets or invoices of TV sets.
Figure 2: Category labels as they stand have a very broad meaning. Only in certain applications or contexts they reflect objects of a clearly defined type.
Figure 3: Often, the hierarchical relations are equivalent to subClassOf in some contexts only.
Now, deriving useful ontologies from hierarchical categorizations for the Semantic Web requires that we derive ontology classes from the categories so that the classes have a clearly defined meaning, i.e. so that they don’t tangle completely different types of objects. At the same time, we may want to preserve the original hierarchical order, since it can be useful for querying using generalizations. Unfortunately, we do not know ex ante whether the original hierarchy is equivalent to subClassOf in a given target context (even if it was equivalent for the broad interpretation of the categories as shown in Figure 2).
Figures 4 and 5 show how GenTax solves this problem:
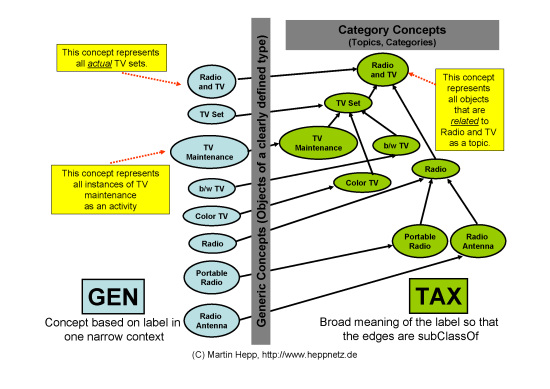
First, GenTax creates two ontology classes per each category (Figure 4): One for the broad category in the context of the original hierarchy (shown in green in Figure 4) and a related second class for the narrower meaning of the category in a particular context (shown in light blue in Figure 4). The second class is a subClass of the category class (this holds in most cases but is evaluated later anyway).
Figure 4: GenTax creates two ontology classes per each category.
Second, GenTax inserts subClassOf relations between all category classes that are subcategories in the original hierarchical categorization scheme (Figure 5). This allows for exploiting the original hierarchy for queries and other operations on the data.
Figure 5: The original hierarchical order is represented by subClassOf relations between the green category classes.
Also, each generic class (in light blue) becomes a subclass of its respective category class.
Figure 6 shows how the original hierarchical categorization schema from Figure 1 would look like after applying the GenTax algorithm.
Figure 6: The schema from Figure 1 after applying the GenTax algorithm.
Now, one may ask how the semantics of the generic classes is determined. First, it is important that we do currently not specify the semantics of those classes axiomatically, though this can be added later. For the moment, we just define suitable extended labels and descriptions in text for those categories (e.g. the label "TV set" becomes "TV set Topic: Anything that can in any relevant context be classified under the respective label" for the category class and "TV set - An actual product of this type" for the generic class). We are considering many extensions of this, e.g. grounding in PROTON etc.
Figure 7 gives a more formal definition of the approach. Formally, the generic classes are defined by the intersection of the category class and a so-called "Master Concept" to be chosen by a human. The Master Concept is the intended super-concept of all generic classes. For example, when deriving an ontology of products and services from the hierarchical schema shown in Figure 1, the master concept would be "An actual product or service". Implicitly, there exists also such a Master Concept for the category classes. By default, its semantics is approximately "Anything that can in any relevant context be classified under the respective label". However, one may want to narrow down this one, too.
In order to make sure that the resulting subsumption hierarchy is correct, one should check the appropriateness of the subClassOf relations between the resulting classes. As said, GenTax suggests using representative random samples for that task.
Figure 7: The GenTax approach in a more formal way.
[1] Hepp, Martin; de Bruijn, Jos: GenTax: A Generic Methodology for Deriving OWL and RDF-S Ontologies from Hierarchical Classifications, Thesauri, and Inconsistent Taxonomies, Proceedings of the 4th European Semantic Web Conference (ESWC 2007), June 3-7, Innsbruck, Austria, Springer LNCS Vol. 4519, Springer 2007, pp.129-144.
http://www.heppnetz.de/files/hepp-de-bruijn-ESWC2007-gentax-CRC.pdf
[2] ESWC 2007 presentation